POLYÈDRES À FACES ARTICULÉES
Polyèdre
Un polyèdre peut être défini de plusieurs manières. Par exemple, les polyèdres ont souvent été définis comme des solides. Cependant, ils ont aussi été définis comme un ensemble de surfaces rigides reliées à leurs arêtes par des charnières. La construction résultante est généralement rigide, avec quelques rares exceptions. Les polyèdres peuvent aussi être définis comme des treillis (frameworks), qui sont obtenus en plaçant des barres aux arêtes, ces barres étant connectées aux sommets par des articulations sphériques. Si toutes les faces sont triangulaires, le treillis est très généralement rigide. Dans les autres cas, le treillis est mobile et perd sa forme polyédrale initiale une fois déformé. De l'information générale sur les polyèdres peut être trouvée à Wikipédia, à The Pavilion of Polyhedreality et à Wolfram MathWorld.

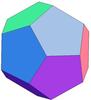
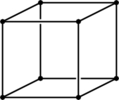

Fig. 1 : Dodécaèdre solide et treillis cubique.
Définition
Ici, une nouvelle définition est proposée. Considérer un polyèdre comme un treillis pour lequel les faces sont contraintes à demeurer planes. La construction résultante est appelée polyèdre à faces articulées (PFA). Dans certains cas les PFAs sont des structures rigides, alors que dans d'autres ils sont des mécanismes articulés, possédant des propriétés cinématiques intéressantes.
Construction
L'implantation de la contrainte de planéité de façon mécanique dans un treillis serait difficile. À la place, il est proposé ici de repartir à zéro avec une nouvelle construction mécanique, qui est protégée par le brevet américain (No. 7,118,442). Premièrement, les faces sont construites comme des mécanismes plans à boucle fermée utilisant un ensemble de pièces formant les côtés des polygones. Ces pièces sont reliées par des articulations rotoïdes aux coins, les axes des articulations étant perpendiculaires au plan formé par la face. Ceci assure la planéité des faces pour toute configuration. Par la suite, les côtés des faces sont reliées par des articulations rotoïdes qui reposent sur les arêtes du polyèdre et intersectent les articulations de faces aux coins de ces faces. Ainsi, toutes les articulations associées à un sommet donné du polyèdre s'intersectent au sommet pour toute configuration. Il est à noter que la construction des PFAs ne requiert qu'un seul type de pièce. De plus, pour les PFAs dans lesquels tous les arêtes ont la même longueur, toutes les pièces sont identiques.
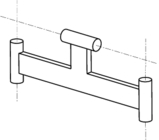
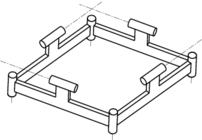
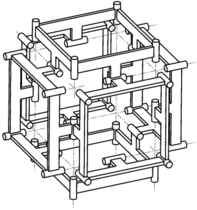
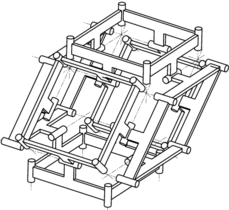
Fig. 2 : Construction d'un PFA cubique : pièce, polygone et deux configurations du polyèdre.
Mobilité
Le principal intérêt des PFAs est que certains peuvent se déformer. Dans certains cas les PFAs sont des structures rigides, alors que dans d'autres ils sont des mécanismes articulés, possédant des propriétés cinématiques intéressantes. Aussi, certains d'entre eux sont localement mobiles mais globalement rigides. En d'autres mots, ils ne peuvent bouger que dans leur configuration initiale. Une chaîne cinématique avec de telles propriétés, ce qui est relativement rare, est souvent appelée chancelante (shaky). Ainsi, une méthode générale a été développée afin de déterminer la mobilité des PFAs, c'est-à-dire combien de degrés de liberté ils possèdent. La méthode utilise la première dérivée des équations de contraintes. Aussi, des simulations numériques sont performées afin d'observer les configurations déformées ou afin de trouver les PFA qui sont chancelants. Finalement, des modèles en plastique sont construits. À cause de la flexibilité du plastique et du jeu aux articulations, les modèles en plastique sont plus flexibles qu'ils devraient l'être en théorie. Ainsi, ils permettent d'observer des configurations déformées des PFAs chancelants, qui ne bougent pratiquement pas en simulation. Il est noté que la plage de mouvement des modèles en plastique est limitée par l'interférence mécanique entre les pièces. Plus de détails sur les PFAs, particulièrement sur l'étude de leur mobilité, peuvent être trouvés dans l'article Polyhedra with Articulated Faces, du congrès IFToMM 2007.
Photos et vidéos
Ici, les PFAs générés à partir des cinq solides de Platon (ou polyèdres réguliers) et des treize solides d'Archimède (ou polyèdres semiréguliers) sont illustrés et leur mobilité est donnée. Les photos des modèles en plastique peuvent être agrandies en cliquant sur l'image.
Solide de Platon
Tétraèdre (4 faces, 6 arêtes, 4 sommets) : rigide
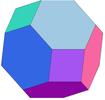
- Cube (6 faces, 12 arêtes, 8 sommets) : mobile (3 ddl)
Octaèdre (8 faces, 12 arêtes, 6 sommets) : rigide
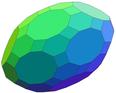
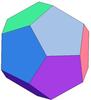
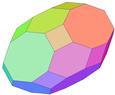
- Dodécaèdre (12 faces, 30 arêtes, 20 sommets) : chancelant (5 ddl)
- Icosaèdre (20 faces, 30 arêtes, 12 sommets) : rigide
Solides d'Archimède
- Tétraèdre tronqué (8 faces, 18 arêtes, 12 sommets) : rigide
- Cuboctaèdre (14 faces, 24 arêtes, 12 sommets) : mobile (3 ddl)
- Octaèdre tronqué (14 faces, 36 arêtes, 24 sommets) : mobile (5 ddl)
- Cube tronqué (14 faces, 36 arêtes, 24 sommets) : rigide
- Rhombicuboctaèdre (26 faces, 48 arêtes, 24 sommets) : mobile (6 ddl)
- Cube adouci (38 faces, 60 arêtes, 24 sommets) : rigide
- Icosidodécaèdre (32 faces, 60 arêtes, 30 sommets) : rigide
- Grand rhombicuboctaèdre (26 faces, 72 arêtes, 48 sommets) : mobile (5 ddl)
- Icosaèdre tronqué (32 faces, 90 arêtes, 60 sommets) : chancelant (5 ddl)
- Dodécaèdre tronqué (32 faces, 90 arêtes, 60 sommets) : chancelant (4 ddl)
- Rhombicosidodécaèdre (62 faces, 120 arêtes, 60 sommets) : mobile (3 ddl) et chancelant (5 ddl)
- Dodécaèdre adouci (92 faces, 150 arêtes, 60 sommets) : rigide


- Grand rhombicosidodécaèdre (62 faces, 180 arêtes, 120 sommets) : mobile (5 ddl)